Como testar a normalidade dos resíduos e a homogeneidade das variâncias

O uso da análise estatística paramétrica, especialmente a análise das variâncias, requer, dentre outras, que a distribuição dos resíduos siga a distribuição normal e que as variâncias sejam homogêneas.

Contudo, caso uma dessas pressuposições não seja atendida, é necessário submeter os dados a transformações de dados dos tipos angular, raiz quadrada e logarítmica, que são as mais conhecidas.

Alguns autores usam o coeficiente de variação como critério de transformação, sendo esse um erro clássico. Abaixo vou ensinar como testar essas pressuposições, usando o programa estatístico SPSS (versão 17).

A técnica que irei ensinar serve tanto para experimentos com um ou mais fatores, tanto para delineamentos inteiramente casualizados (DIC) quanto para o de blocos ao acaso (DBC).

Tela inicial do SPSS

Figura 1. Vá em abrir pasta e busque o arquivo (Excel) que você digitou os dados. Abra clicando no ícone da pasta.

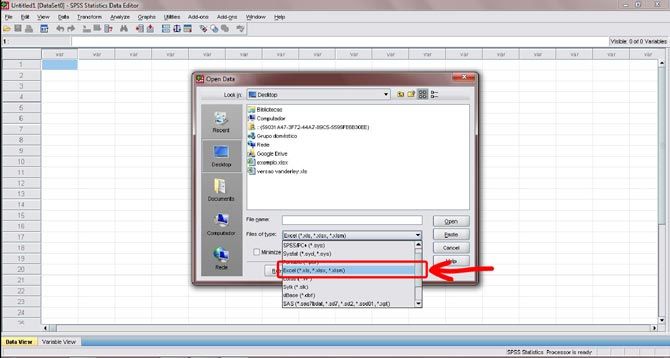
Figura 2. Clique onde está marcado com a seta para mudar o formato de arquivo para o tipo Excel. Após achar seu arquivo, clique em “open” para abrir.

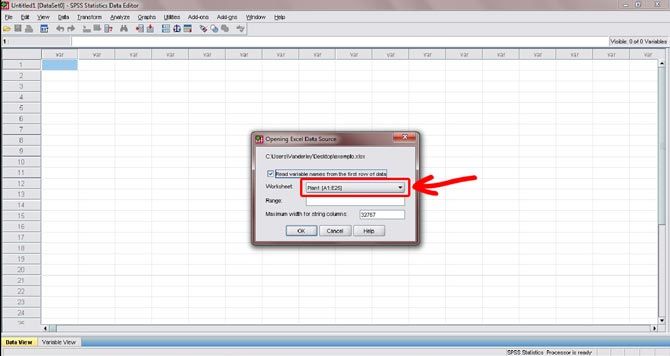
Figura 3. O SPSS abre qualquer aba da planilha original. Selecione na área worksheet a aba em que seus dados foram digitados. Clique em ok.

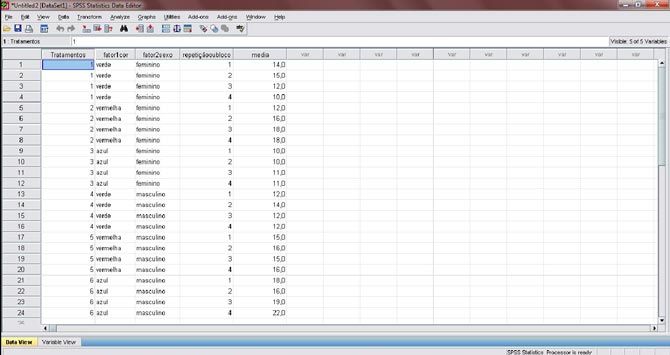
Figura 4. Planilha aberta oriunda do excel. Note que a primeira linha do Excel ficou separada dos valores, elas indicam sobre o quê se trata a coluna.

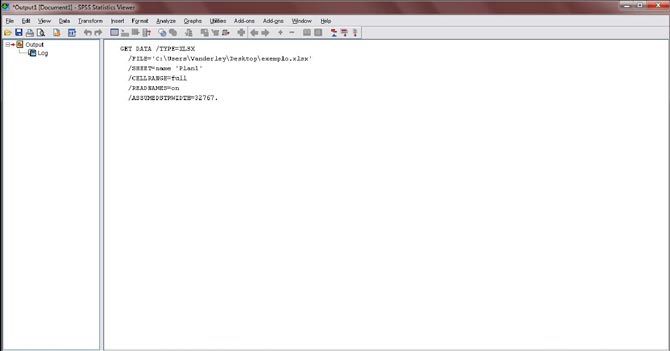
Figura 5. Essa tela abrirá juntamente com a anterior, nela ficarão os resultados da análise.

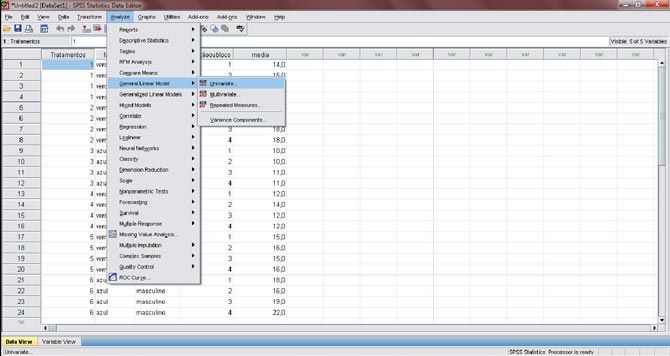
Figura 6. Vá ao menu “Analyze”, em seguida em “General Linear Model” e, por fim, clique em “Univariate”.

HOMOGENEIDADE DAS VARIÂNCIAS

Note que essa pressuposição diz respeito aos resíduos e não aos dados. Assim é necessário calcular os resíduos. Nesse tutorial, explico um modelo com fatorial e com blocos, porém se seu experimento for com apenas um fator ou em DIC, basta ignorar alguns passos.

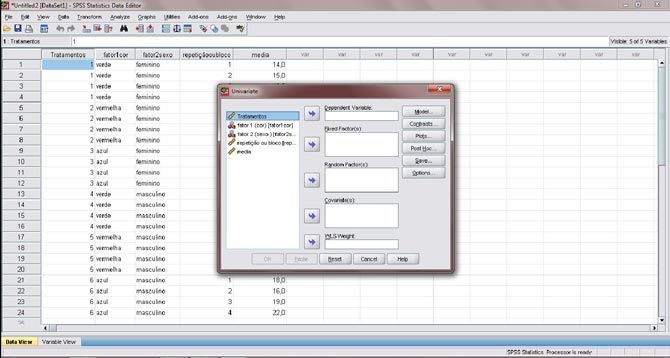
Figura 7. Note que eu preparei a coluna tratamento, que diz respeito a combinações dos fatores cor e sexo (fator 1 e 2, respectivamente), logo, como tenho um fatorial 3 x 2, três cores e dois sexos, eu tenho um total de 6 tratamentos na coluna tratamento. Caso seu experimento seja com um fator, seus tratamentos já são essa coluna.

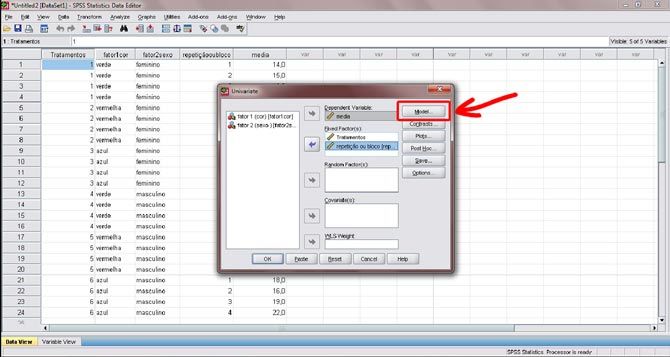
Figura 8. Insira, no fator fixo, a variável que você definiu para testar, no caso, será a coluna “Tratamentos” para experimentos fatoriais. Caso seus dados sejam oriundos de um experimento com único fator, entre com a coluna que descreve os tratamentos. No exemplo acima, é necessário entrar também com os blocos, pois o delineamento é um DBC. Para o caso dos experimentos em DIC, é necessário deixar somente os tratamentos. Na variável dependente coloque a variável resposta, ou seja, a variável que será testada. No exemplo, a variável dependente diz respeito à média das observações, portanto, a variável “média” foi inserida no campo “Dependent Variable”. Feito isso, clique no botão “Model”.

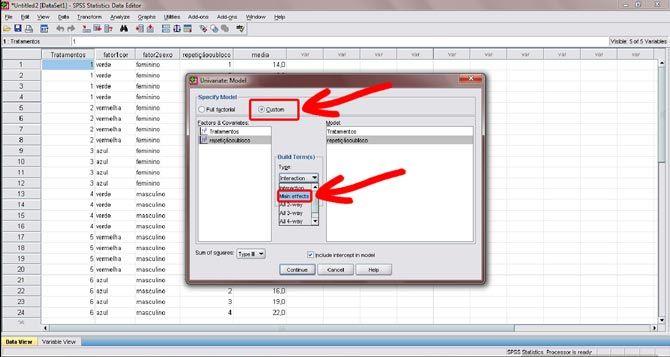
Figura 9. Marque a opção “custom”, destacada pela seta em azul. Em seguida, na área “Factors & Covariates”, selecione os itens “Tratamentos” e “repetição ou bloco” e na seção “Build Term(s)”, marque a opção “Main effects” (seta vermelha), já que nesse momento o que nos interessa são os efeitos principais das variáveis. Feito isso, clique em OK. Obs.: Caso seu experimento seja em DIC, não entre nessa página e pule para a próxima etapa.

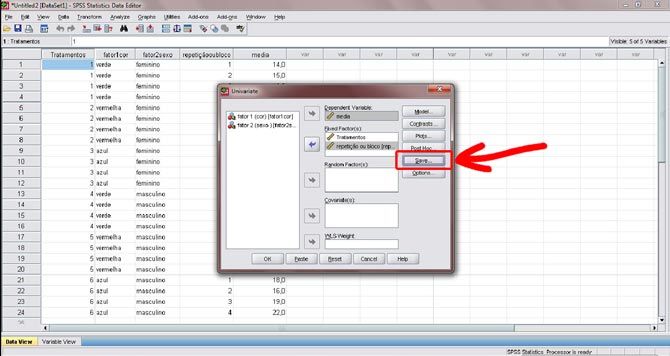
Figura 10. Clique no botão “Save”.

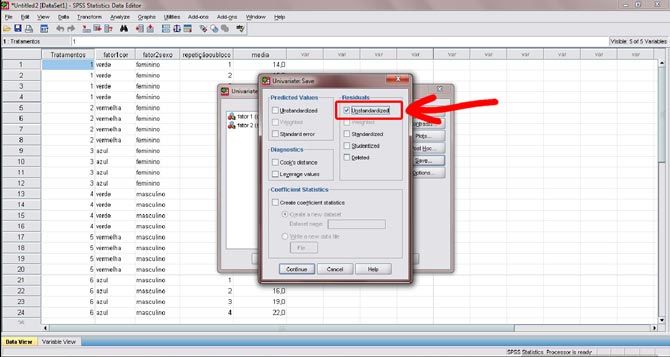
Figura 11. Na nova janela, na área “Residuals”, selecione que você deseja resíduos não padronizados (opção “unstandardized”, à esquerda da seta azul) e clique em continuar.

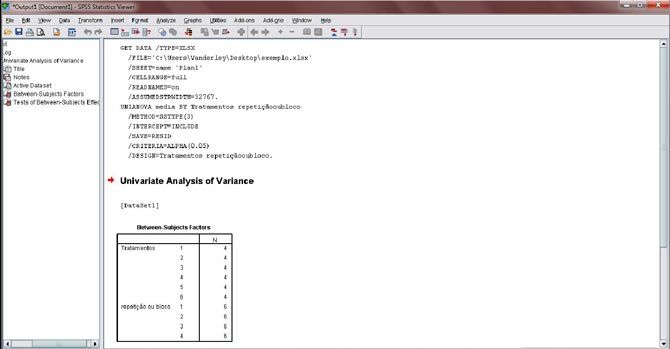
Figura 12. A tela de output (resultados) será aberta. Como vamos analisa-la com cuidado posteriormente, minimize-a por enquanto.

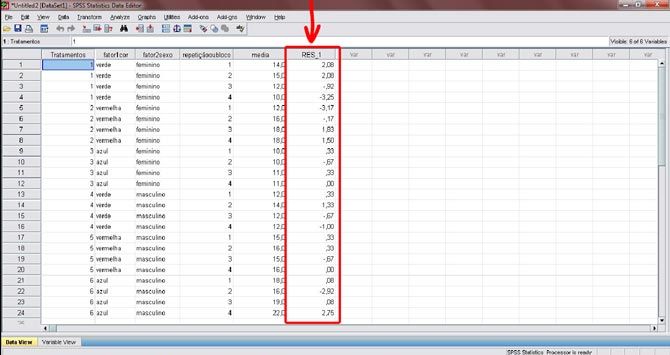
Figura 13. Ao retornar para a tela onde os dados são exibidos, você perceberá que os resíduos das observações foram calculados. Esses novos dados aparecerão na coluna “RES_1” (abaixo da seta). Siga novamente as recomendações da figura 6 e, em seguida, prossiga para a próxima figura.

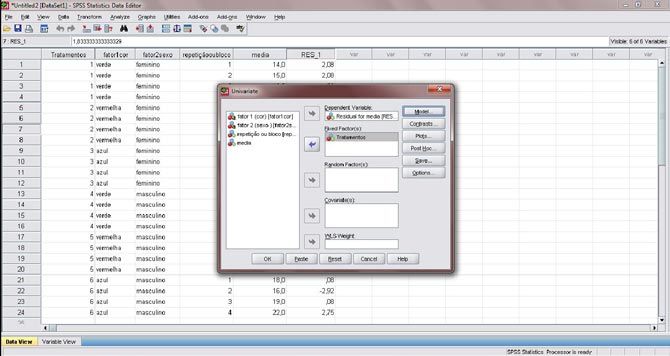
Figura 14. Agora, será necessário retirar os blocos dos fatores fixos e colocar os resíduos das observações no campo “Dependent Variable”. Após isso, clique no botão “save”.

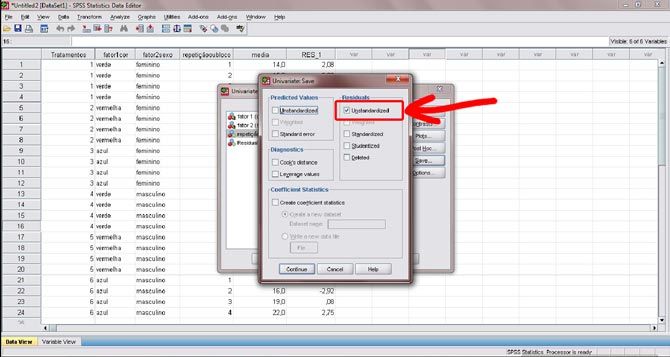
Figura 15. Na nova janela, na área “Residuals”, desmarque a opção “untandartized”, referente aos resíduos não padronizados, calculados anteriormente. Em seguida, clique no botão “Continue”.

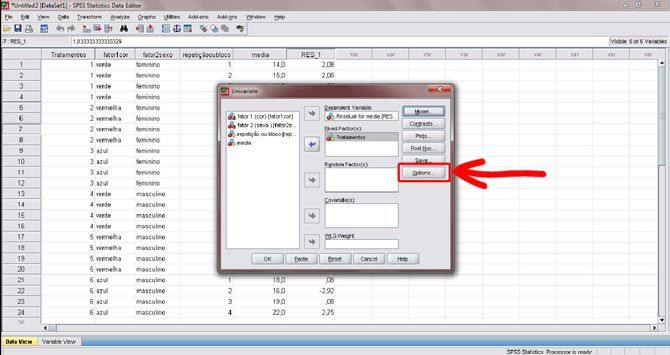
Figura 16. De volta à janela principal “Univariate”, clique agora no botão “options”.

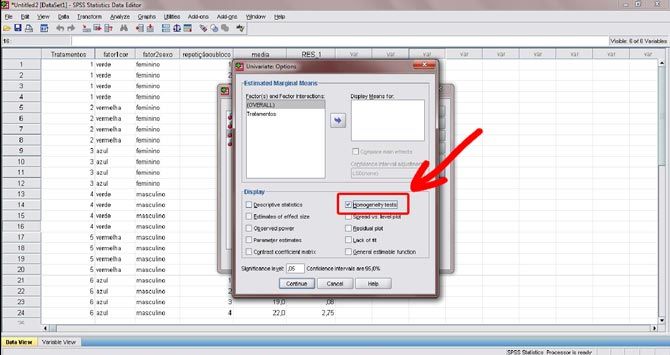
Figura 17. Na nova janela, marque a opção “homogeneity test”, já que agora faremos o teste de homogeneidade, e clique no botão “continue”.

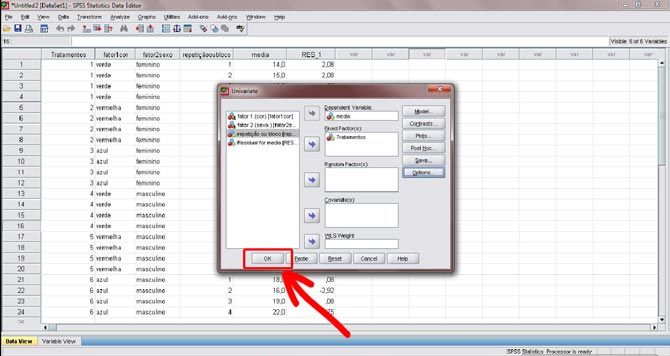
Figura 18. Finalmente, clique no botão “ok”.

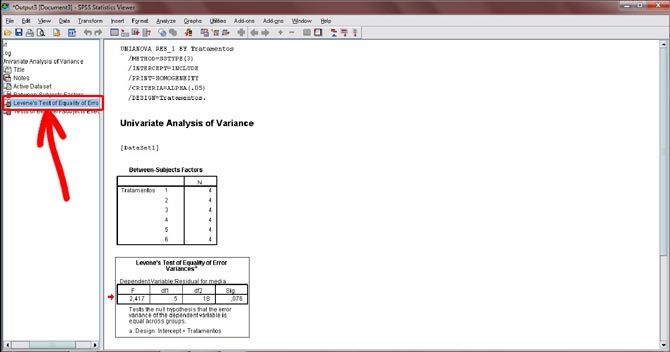
Figura 19. A tela de output (resultados) será novamente aberta. Desta vez, clique na opção “Lenenes’s test”, situada à esquerda dos resultados e marcada com a seta.

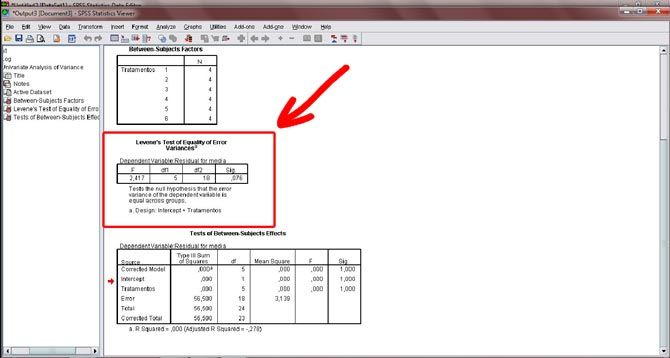
Figura 20. O resultado do teste de Levene é apresentado. No caso da amostra de exemplo, o valor de significância (Sig) do experimento foi de 0,076, ou seja, há homogeneidade de variâncias. Lembrando que, caso a significância de sua amostra apresente um resultado abaixo de 0,05, as variâncias seriam heterogêneas, o que leva a possibilidade de realizar transformações nos dados.

NORMALIDADE DOS RESÍDUOS

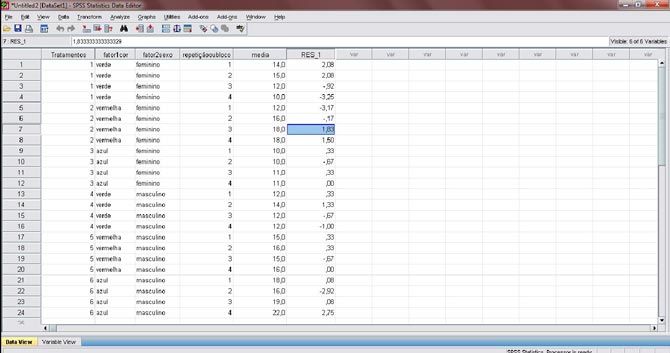
Figura 21. Volte a tela inicial do SPSS, onde os dados são exibidos.

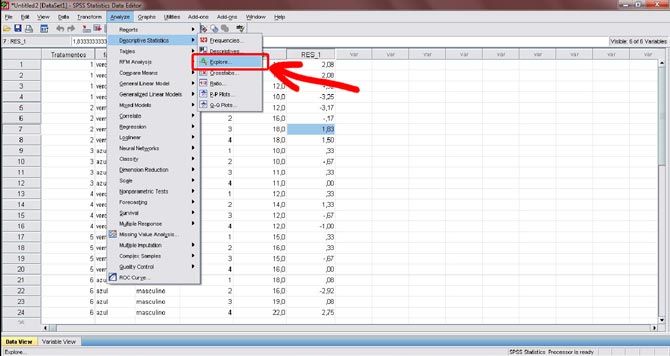
Figura 22. Agora, já que observados que a variância é homogênea, calcularemos a normalidade dos resíduos. Para isso, clique no menu “Analyze” e, em seguida, em “Descriptive Statistics” e por fim em “Explore”.

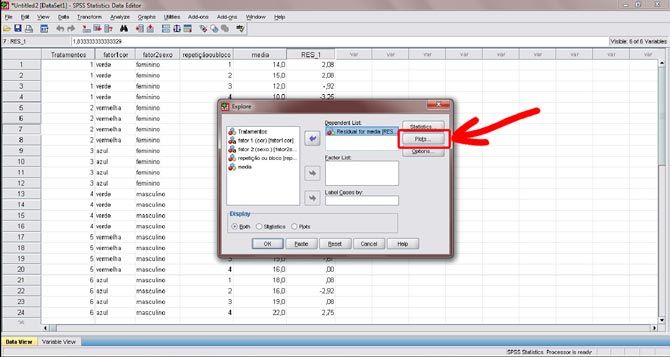
Figura 23. Na nova janela, insira os resíduos anteriormente calculados na seção “dependent list” (no caso do exemplo, trata-se da coluna “RES_1”). Por fim, clique no botão “Plots”.

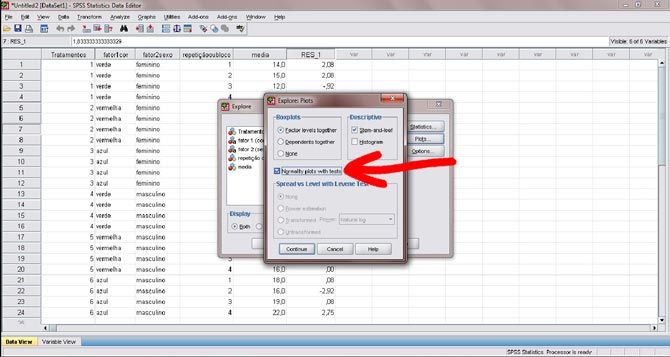
Figura 24. Na nova janela, marque a opção “Normally plots with tests”, destacada pela seta (essa opção diz respeito ao teste de normalidade dos resíduos). Em seguida, clique no botão “continue”.

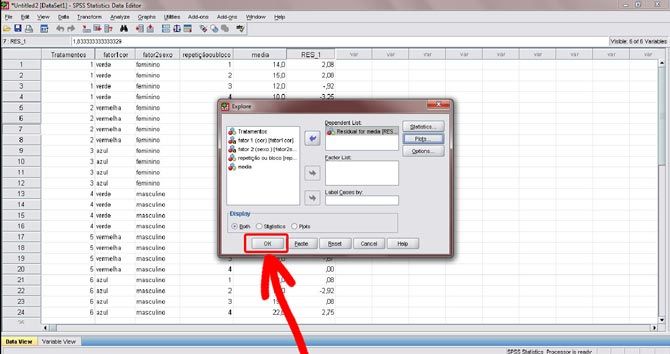
Figura 25. De volta à janela “Explore”, clique no botão “OK”.

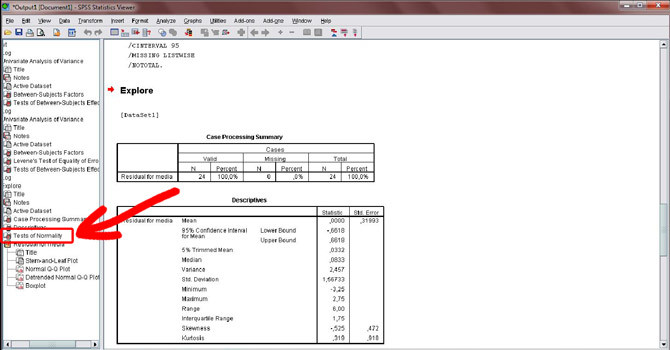
Figura 26. Novamente, a tela de resultados é aberta. Clique em “Test of normality”, indicado pela seta.

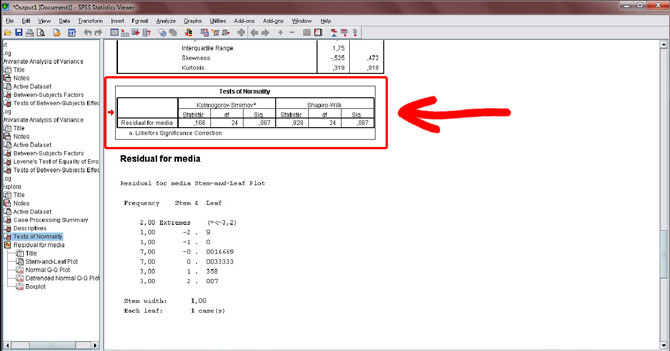
Figura 27. O teste de normalidade dos resíduos é apresentado. É interessante destacar que o SPSS calcula tanto o teste de Kolmogorov-Smirnov com a correção de Lilliefors, quanto o de Shapiro-Wilk (ambos são diferentes testes de normalidade).

No caso deste exemplo, ambos os testes apresentaram significância (Sig) de 0,087, ou seja, a amostra possui resíduos com distribuição normal. Lembrando que, caso a significância de sua amostra apresente um resultado abaixo de 0,05, ela não possui uma distribuição normal dos resíduos, o que leva a possibilidade de realizar transformações nos dados.